Le concept de « corps noir » est central en physique et en thermodynamique : il a joué un rôle historique dans la naissance de la mécanique quantique. Cet article explique, de façon simple et pédagogique, ce qu’est un corps noir, pourquoi il posait un problème aux physiciens du XIXe siècle, et comment la mécanique quantique a résolu l’énigme.

Qu’est-ce que c’est ?

Un « corps noir » est un objet idéal qui absorbe parfaitement toute la lumière (ou, plus généralement, tout rayonnement électromagnétique) qui tombe sur lui, sans en réfléchir ni en transmettre. Autrement dit, à toutes les longueurs d’onde, l’absorptivité est égale à 1. Par un argument d’équilibre thermodynamique, un corps noir parfait est aussi le meilleur émetteur possible à une température donnée : il émet un spectre de rayonnement qui dépend uniquement de sa température, et non de sa composition ou de sa forme.

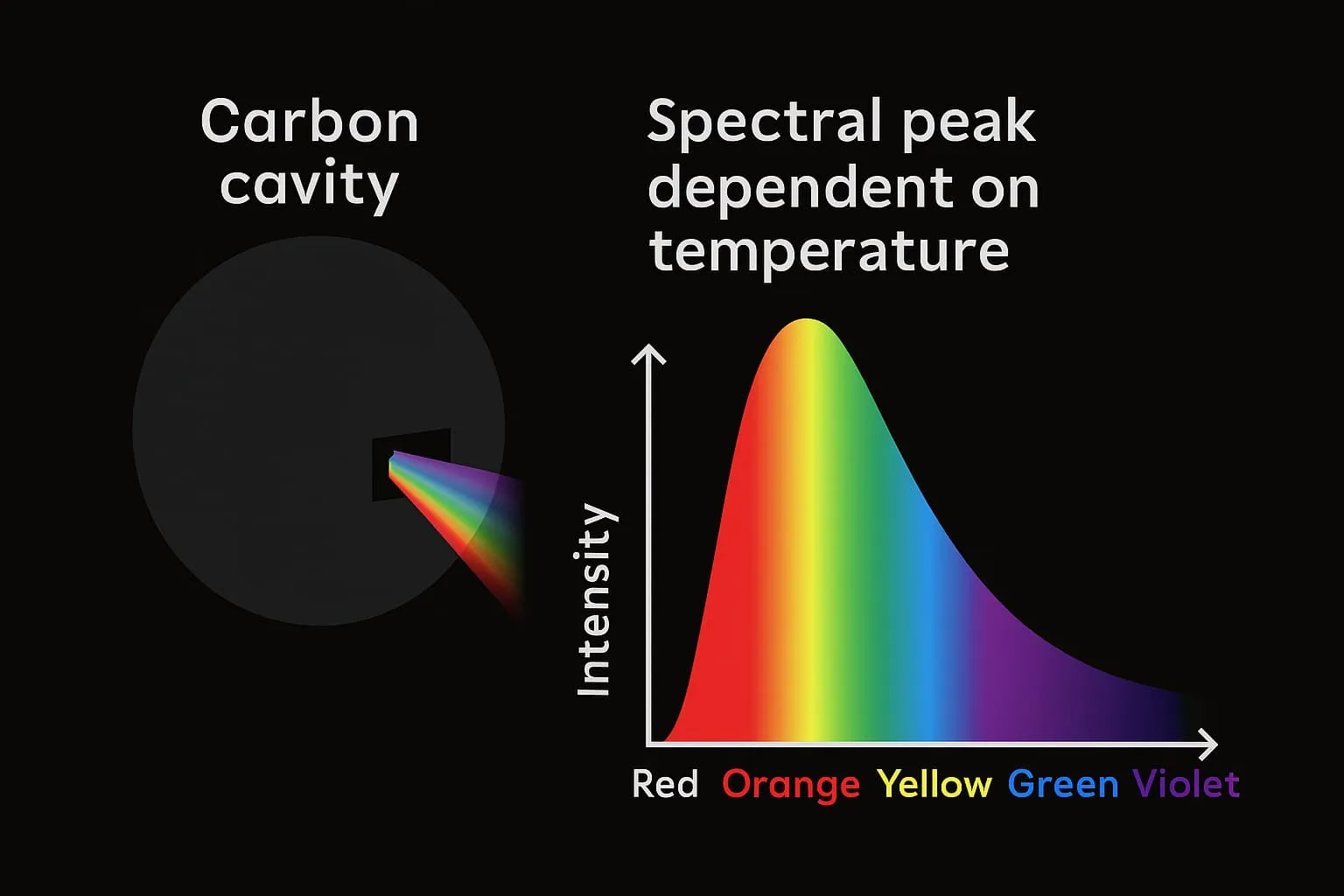
Dans la réalité, on ne trouve pas de corps noir parfait, mais certains dispositifs s’en rapprochent beaucoup. L’exemple classique est une cavité fermée avec une petite ouverture : la lumière qui entre par l’ouverture subit de nombreuses réflexions à l’intérieur et a très peu de chances de ressortir, ce qui fait de l’ouverture un excellent absorbeur — et la cavité, vue de l’extérieur, se comporte comme un corps noir.

Pourquoi s’intéresser à ce modèle ? Parce que le rayonnement émis par un corps noir contient une signature précise de la température : mesurer ce rayonnement permet de connaître la température d’un astre (comme une étoile) ou d’un objet chaud. De plus, l’étude de ce spectre a conduit à des découvertes fondamentales sur la nature de la lumière et de l’énergie.

Quelques notions utiles pour comprendre le problème :

• Spectre : la distribution de l’énergie émise en fonction de la longueur d’onde (ou de la fréquence). Un corps noir à température T a un spectre particulier — appelé spectre du corps noir — qui montre à quelles longueurs d’onde l’essentiel de l’énergie est émis.
• Loi de Stefan–Boltzmann : l’énergie totale émise par unité de surface d’un corps noir est proportionnelle à T^4 (T en kelvins). Cette loi est empirique puis déduite théoriquement.
• Loi de Wien : la longueur d’onde pour laquelle l’intensité est maximale varie inversement avec la température (plus l’objet est chaud, plus le pic du spectre se déplace vers les courtes longueurs d’onde).

La résolution du problème

À la fin du XIXe siècle, les physiciens cherchaient à prédire théoriquement le spectre du rayonnement d’un corps noir. Les méthodes de la physique classique permettaient d’obtenir une expression (la loi de Rayleigh–Jeans) qui fonctionnait bien pour les grandes longueurs d’onde (rouge, infra‑rouge), mais qui prédisait une énergie infinie quand on intégrait sur toutes les longueurs d’onde : c’était la fameuse “catastrophe ultraviolette”. En clair, la théorie classique disait que les corps noirs devraient émettre une quantité d’énergie illimitée à haute fréquence — ce que l’expérience démentait.

En 1900, Max Planck proposa une hypothèse audacieuse pour résoudre l’énigme : l’énergie des oscillateurs qui émettent le rayonnement (au sein des parois de la cavité) n’est pas continue, mais quantifiée. Autrement dit, ces oscillateurs ne peuvent échanger de l’énergie qu’en paquets discrets d’énergie E = hν, où ν est la fréquence et h est une constante universelle (la constante de Planck).

En introduisant cette quantification dans le calcul statistique du rayonnement, Planck dériva une loi pour le spectre du corps noir (la loi de Planck) qui s’accorde parfaitement avec les observations : elle tend vers la loi de Rayleigh–Jeans aux basses fréquences et décroît exponentiellement aux hautes fréquences, évitant ainsi la catastrophe ultraviolette.

Pourquoi est‑ce important ? Parce que la quantification introduite par Planck a été le premier indice sérieux que l’énergie n’est pas toujours continue à l’échelle microscopique. Cette idée a ouvert la voie à la mécanique quantique : les concepts d’états discrets, de quanta d’énergie, et plus tard, la dualité onde‑particule et la formulation moderne de la mécanique quantique.

Quelques points d’intuition :

• Penser à des oscillateurs (comme de petites masses sur des ressorts) : en mécanique classique, ces oscillateurs peuvent avoir n’importe quelle énergie. En imposant que l’énergie ne peut être un multiple entier de hν, on réduit le nombre d’états accessibles à haute fréquence, ce qui diminue l’énergie totale prédite.
• Le spectre du corps noir est universel : deux cavités à la même température ont le même spectre, même si elles sont faites de matériaux différents. C’est une propriété d’équilibre thermodynamique qui a rendu le problème si fondamental.
• La constante de Planck h est extrêmement petite. Pour des objets usuels (température ambiante, fréquences basses), les effets de quantification ne se remarquent pas — d’où la réussite de la physique classique à grande échelle. Mais pour la lumière visible et ultraviolette, l’hypothèse de Planck devient cruciale.

Conclusion

Le problème du rayonnement du corps noir est un bel exemple où une difficulté expérimentale a forcé une remise en cause des principes établis. La solution de Planck n’était pas seulement une « rustine » mathématique : elle a inauguré une nouvelle façon de penser l’énergie et la matière. Comprendre le corps noir, c’est comprendre une étape clé de l’histoire de la physique et la naissance de la mécanique quantique — une leçon de prudence : les intuitions continues de la physique classique ne suffisent pas toujours pour décrire l’infiniment petit.

Références et lectures conseillées :

• Max Planck (1901) — “Sur la loi de distribution de l’énergie dans le spectre du rayonnement” (article historique ; résumé dans la plupart des manuels).
• Pour aller plus loin : un bon manuel d’introduction à la physique moderne ou une ressource de vulgarisation sur la mécanique quantique.